Time Dilation Calculator
Calculates the time dilation of an object moving for some time with some relative velocity with respect to the observer.
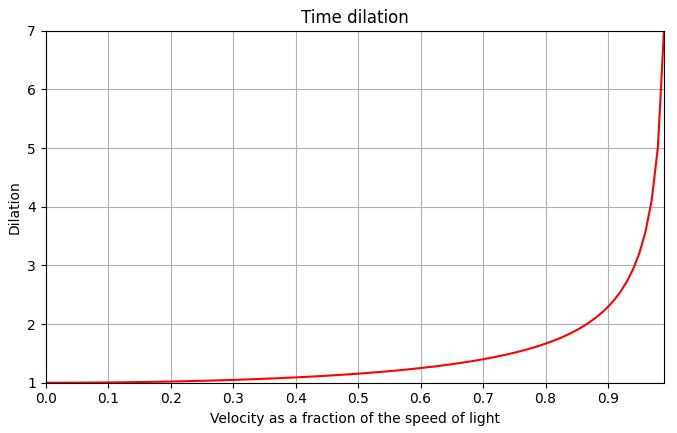
$$t = {t0 \over \sqrt{1 - {v \over c}^2}}$$t = time observed in the other reference frame
t0 = time observed in the moving object's reference frame
v = the speed of the moving object
c = the speed of light
An astronaut boards a spaceship and travels through space at 95% the speed of light (v) for 1 year (t0). When the journey is complete,
a clock on earth (t) is compared with the spaceship's clock (t0). The clock on earth shows that the journey took 3.2 years, but the clock
on board the ship shows that the journey took 1 year.
t = t0 / sqrt(1 - (v / c)²)
t = 1 / sqrt(1 - (.95 / 1)²)
t = 1 / sqrt(1 - .95²)
t = 1 / sqrt(1 - .9025)
t = 1 / sqrt(0.0975)
t = 1 / 0.3122
t = 3.2